The Higgs boson or Higgs particle is an elementary particle in the Standard Model of particle physics. Observation of the particle allows scientists to explore the Higgs field[6][7]├óŌé¼ŌĆØa fundamental field of crucial importance to particle physics theory,[7] first suspected to exist in the 1960s, that unlike other known fields such as the electromagnetic field, takes a non-zero constant value almost everywhere. For several decades the question of the Higgs Field's existence was the last unverified part of the Standard Model of particle physics and "the central problem in particle physics".[8][9] The presence of this field, now believed to be confirmed, explains why some fundamental particles have mass when, based on the symmetries controlling their interactions, they should be massless. It also solves several other long-standing puzzles, such as the reason for the weak force's extremely short range.
Despite being present everywhere, the existence of the Higgs field is very hard to confirm. It can be detected through its excitations (i.e. Higgs particles), but these are extremely hard to produce and detect. The importance of this fundamental question led to a 40 year search, and the construction of one of the world's most expensive and complex experimental facilities to date, CERN's Large Hadron Collider,[10] able to create Higgs bosons and other particles for observation and study. On 4 July 2012, the discovery of a new particle with a mass between 125 and 127 GeV/c2 was announced; physicists suspected that it was the Higgs boson.[11][12][13] By March 2013, the particle had been proven to behave, interact and decay in many of the ways predicted by the Standard Model, and was also tentatively confirmed to have even parity and zero spin,[1] two fundamental attributes of a Higgs boson. This appears to be the first elementary scalar particle discovered in nature.[14] More data is needed to know if the discovered particle exactly matches the predictions of the Standard Model, or whether, as predicted by some theories, multiple Higgs bosons exist.[3]
The Higgs boson is named after Peter Higgs, one of six physicists who, in 1964, proposed the mechanism that suggested the existence of such a particle. On December 10, 2013 two of these, Peter Higgs and Fran├ā┬¦ois Englert, were awarded the Nobel Prize in Physics for their work and prediction (Englert's co-researcher Robert Brout had died in 2011 and the Nobel Prize is not ordinarily given posthumously).[15] Although Higgs's name has come to be associated with this theory, several researchers between about 1960 and 1972 each independently developed different parts of it. In mainstream media the Higgs boson has often been called the "God particle", from a 1993 book on the topic; the nickname is strongly disliked by many physicists, including Higgs, who regard it as inappropriate sensationalism.[16][17][18]
In the Standard Model, the Higgs particle is a boson with no spin, electric charge, or colour charge. It is also very unstable, decaying into other particles almost immediately. It is a quantum excitation of one of the four components of the Higgs field. The latter constitutes a scalar field, with two neutral and two electrically charged components, and forms a complex doublet of the weak isospin SU(2) symmetry. The Higgs field is tachyonic (this does not refer to faster-than-light speeds, it means that symmetry-breaking through condensation of a particle must occur under certain conditions), and has a "Mexican hat" shaped potential with nonzero strength everywhere (including otherwise empty space), which in its vacuum state breaks the weak isospin symmetry of the electroweak interaction. When this happens, three components of the Higgs field are "absorbed" by the SU(2) and U(1) gauge bosons (the "Higgs mechanism") to become the longitudinal components of the now-massive W and Z bosons of the weak force. The remaining electrically neutral component separately couples to other particles known as fermions (via Yukawa couplings), causing these to acquire mass as well. Some versions of the theory predict more than one kind of Higgs fields and bosons. Alternative "Higgsless" models would have been considered if the Higgs boson was not discovered.
Overview
In particle physics, elementary particles and forces give rise to the world around us. Nowadays, physicists explain the behaviour of these particles and how they interact using the Standard Model├óŌé¼ŌĆØa widely accepted and "remarkably" accurate[21] framework based on gauge invariance and symmetries, believed to explain almost everything in the world we see, other than gravity.[22]
But by around 1960 all attempts to create a gauge invariant theory for two of the four fundamental forces had consistently failed at one crucial point: although gauge invariance seemed extremely important, it seemed to make any theory of electromagnetism and the weak force go haywire, by demanding that either many particles with mass were massless or that non-existent forces and massless particles had to exist. Scientists had no idea how to get past this point.
In 1962 physicist Philip Anderson wrote a paper that built upon work by Yoichiro Nambu concerning "broken symmetries" in superconductivity and particle physics. He suggested that "broken symmetries" might also be the missing piece needed to solve the problems of gauge invariance. In 1964 a theory was created almost simultaneously by 3 different groups of researchers, that showed Anderson's suggestion was possible - the gauge theory and "mass problems" could indeed be resolved if an unusual kind of field existed throughout the universe; if this kind of field did exist, it would apparently cause existing particles to acquire mass instead of new massless particles being formed. Although these ideas did not gain much initial support or attention, by 1972 it had been developed into a comprehensive theory and proved capable of giving "sensible" results that were extremely accurate, including very accurate predictions of several other particles discovered during the following years.[Note 7] During the 1970s these theories rapidly became the "standard model" favoured by physicists and used to describe particle physics and particle interactions in nature. There was not yet any direct evidence that this field actually existed, but even without proof of the field, the accuracy of its predictions led scientists to believe the theory might be true. By the 1980s the question whether or not such a field existed and whether this was the correct explanation, was considered to be one of the most important unanswered questions in particle physics, and by the 1990s two of the largest experimental installations ever created were being designed and constructed to find the answer.
If this new kind of field did exist in nature, it would be a monumental discovery for science and human knowledge, and would open doorways to new knowledge in many disciplines. If not, then other more complicated theories would need to be explored. The simplest solution to whether the field existed was by searching for a new kind of particle it would have to give off, known as "Higgs bosons" or the "Higgs particle". These would be extremely difficult to find, so it was only many years later that experimental technology became sophisticated enough to answer the question.
While several symmetries in nature are spontaneously broken through a form of the Higgs mechanism, in the context of the Standard Model the term "Higgs mechanism" almost always means symmetry breaking of the electroweak field. It is considered confirmed, but revealing the exact cause has been difficult.
Various analogies have also been invented to describe the Higgs field and boson, including analogies with well-known symmetry breaking effects such as the rainbow and prism, electric fields, ripples, and resistance of macro objects moving through media, like people moving through crowds or some objects moving through syrup or molasses. However, analogies based on simple resistance to motion are inaccurate as the Higgs field does not work by resisting motion.

Theoretical need for the Higgs
Gauge invariance is an important property of modern particle theories such as the Standard Model, partly due to its success in other areas of fundamental physics such as electromagnetism and the strong interaction (quantum chromodynamics). However, there were great difficulties in developing gauge theories for the weak nuclear force or a possible unified electroweak interaction. Fermions with a mass term would violate gauge symmetry and therefore cannot be gauge invariant. (This can be seen by examining the Dirac Lagrangian for a fermion in terms of left and right handed components; we find none of the spin-half particles could ever flip helicity as required for mass, so they must be massless.[Note 13]) W and Z bosons are observed to have mass, but a boson mass term contains terms, which clearly depend on the choice of gauge and therefore these masses too cannot be gauge invariant. Therefore it seems that none of the standard model fermions or bosons could "begin" with mass as an inbuilt property except by abandoning gauge invariance. If gauge invariance were to be retained, then these particles had to be acquiring their mass by some other mechanism or interaction. Additionally, whatever was giving these particles their mass, had to not "break" gauge invariance as the basis for other parts of the theories where it worked well, and had to not require or predict unexpected massless particles and long-range forces (seemingly an inevitable consequence of Goldstone's theorem) which did not actually seem to exist in nature.
A solution to all of these overlapping problems came from the discovery of a previously unnoticed borderline case hidden in the mathematics of Goldstone's theorem,[Note 11] that under certain conditions it might theoretically be possible for a symmetry to be broken without disrupting gauge invariance and without any new massless particles or forces, and having "sensible" (renormalisable) results mathematically: this became known as the Higgs mechanism.
The Standard Model hypothesizes a field which is responsible for this effect, called the Higgs field (symbol: \phi), which has the unusual property of a non-zero amplitude in its ground state; i.e., a non-zero vacuum expectation value. It can have this effect because of its unusual "Mexican hat" shaped potential whose lowest "point" is not at its "centre". Below a certain extremely high energy level the existence of this non-zero vacuum expectation spontaneously breaks electroweak gauge symmetry which in turn gives rise to the Higgs mechanism and triggers the acquisition of mass by those particles interacting with the field. This effect occurs because scalar field components of the Higgs field are "absorbed" by the massive bosons as degrees of freedom, and couple to the fermions via Yukawa coupling, thereby producing the expected mass terms. In effect when symmetry breaks under these conditions, the Goldstone bosons that arise interact with the Higgs field (and with other particles capable of interacting with the Higgs field) instead of becoming new massless particles, the intractable problems of both underlying theories "neutralise" each other, and the residual outcome is that elementary particles acquire a consistent mass based on how strongly they interact with the Higgs field. It is the simplest known process capable of giving mass to the gauge bosons while remaining compatible with gauge theories.[81] Its quantum would be a scalar boson, known as the Higgs boson.[82]
Properties of the Higgs boson
Since the Higgs field is scalar, the Higgs boson has no spin. The Higgs boson is also its own antiparticle and is CP-even, and has zero electric and colour charge.[90]
The Minimal Standard Model does not predict the mass of the Higgs boson.[91] If that mass is between 115 and 180 GeV/c2, then the Standard Model can be valid at energy scales all the way up to the Planck scale (1019 GeV).[92] Many theorists expect new physics beyond the Standard Model to emerge at the TeV-scale, based on unsatisfactory properties of the Standard Model.[93] The highest possible mass scale allowed for the Higgs boson (or some other electroweak symmetry breaking mechanism) is 1.4 TeV; beyond this point, the Standard Model becomes inconsistent without such a mechanism, because unitarity is violated in certain scattering processes.[94]
It is also possible, although experimentally difficult, to estimate the mass of the Higgs boson indirectly. In the Standard Model, the Higgs boson has a number of indirect effects; most notably, Higgs loops result in tiny corrections to masses of W and Z bosons. Precision measurements of electroweak parameters, such as the Fermi constant and masses of W/Z bosons, can be used to calculate constraints on the mass of the Higgs. As of July 2011, the precision electroweak measurements tell us that the mass of the Higgs boson is likely to be less than about 161 GeV/c2 at 95% confidence level (this upper limit would increase to 185 GeV/c2 if the lower bound of 114.4 GeV/c2 from the LEP-2 direct search is allowed for[95]). These indirect constraints rely on the assumption that the Standard Model is correct. It may still be possible to discover a Higgs boson above these masses if it is accompanied by other particles beyond those predicted by the Standard Model.[96]
Experimental search
Main article: Search for the Higgs boson
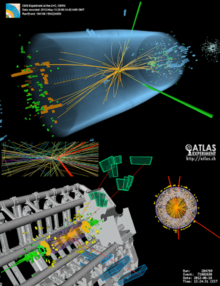
To produce Higgs bosons, two beams of particles are accelerated to very high energies and allowed to collide within a particle detector. Occasionally, although rarely, a Higgs boson will be created fleetingly as part of the collision byproducts. Because the Higgs boson decays very quickly, particle detectors cannot detect it directly. Instead the detectors register all the decay products (the decay signature) and from the data the decay process is reconstructed. If the observed decay products match a possible decay process (known as a decay channel) of a Higgs boson, this indicates that a Higgs boson may have been created. In practice, many processes may produce similar decay signatures. Fortunately, the Standard Model precisely predicts the likelihood of each of these, and each known process, occurring. So, if the detector detects more decay signatures consistently matching a Higgs boson than would otherwise be expected if Higgs bosons did not exist, then this would be strong evidence that the Higgs boson exists.
Because Higgs boson production in a particle collision is likely to be very rare (1 in 10 billion at the LHC),[Note 14] and many other possible collision events can have similar decay signatures, the data of hundreds of trillions of collisions needs to be analysed and must "show the same picture" before a conclusion about the existence of the Higgs boson can be reached. To conclude that a new particle has been found, particle physicists require that the statistical analysis of two independent particle detectors each indicate that there is lesser than a one-in-a-million chance that the observed decay signatures are due to just background random Standard Model events├óŌé¼ŌĆØi.e., that the observed number of events is more than 5 standard deviations (sigma) different from that expected if there was no new particle. More collision data allows better confirmation of the physical properties of any new particle observed, and allows physicists to decide whether it is indeed a Higgs boson as described by the Standard Model or some other hypothetical new particle.
To find the Higgs boson, a powerful particle accelerator was needed, because Higgs bosons might not be seen in lower-energy experiments. The collider needed to have a high luminosity in order to ensure enough collisions were seen for conclusions to be drawn. Finally, advanced computing facilities were needed to process the vast amount of data (25 petabytes per year as at 2012) produced by the collisions.[109] For the announcement of 4 July 2012, a new collider known as the Large Hadron Collider was constructed at CERN with a planned eventual collision energy of 14 TeV├óŌé¼ŌĆØover seven times any previous collider├óŌé¼ŌĆØand over 300 trillion (3├āŌĆö1014) LHC proton├óŌé¼ŌĆ£proton collisions were analysed by the LHC Computing Grid, the world's largest computing grid (as of 2012), comprising over 170 computing facilities in a worldwide network across 36 countries.
Particle physics usually has a hard time competing with politics and celebrity gossip for headlines, but the Higgs boson has garnered some serious attention. That's exactly what happened on July 4, 2012, though, when scientists at CERN announced that they'd found a particle that behaved the way they expect the Higgs boson to behave. Maybe the famed boson's grand and controversial nickname, the "God Particle," has kept media outlets buzzing. Then again, the intriguing possibility that the Higgs boson is responsible for all the mass in the universe rather captures the imagination, too. Or perhaps we're simply excited to learn more about our world, and we know that if the Higgs boson does exist, we'll unravel the mystery a little more.
In order to truly understand what the Higgs boson is, however, we need to examine one of the most prominent theories describing the way the cosmos works: the standard model. The model comes to us by way of particle physics, a field filled with physicists dedicated to reducing our complicated universe to its most basic building blocks. It's a challenge we've been tackling for centuries, and we've made a lot of progress. First we discovered atoms, then protons, neutrons and electrons, and finally quarks and leptons (more on those later). But the universe doesn't only contain matter; it also contains forces that act upon that matter. The standard model has given us more insight into the types of matter and forces than perhaps any other theory we have.
Here's the gist of the standard model, which was developed in the early 1970s: Our entire universe is made of 12 different matter particles and four forces [source: European Organization for Nuclear Research]. Among those 12 particles, you'll encounter six quarks and six leptons. Quarks make up protons and neutrons, while members of the lepton family include the electron and the electron neutrino, its neutrally charged counterpart. Scientists think that leptons and quarks are indivisible; that you can't break them apart into smaller particles. Along with all those particles, the standard model also acknowledges four forces: gravity, electromagnetic, strong and weak.
As theories go, the standard model has been very effective, aside from its failure to fit in gravity. Armed with it, physicists have predicted the existence of certain particles years before they were verified empirically. Unfortunately, the model still has another missing piece -- the Higgs boson. What is it, and why is it necessary for the universe the standard model describes to work? Let's find out.
As it turns out, scientists think each one of those four fundamental forces has a corresponding carrier particle, or boson, that acts upon matter. That's a hard concept to grasp. We tend to think of forces as mysterious, ethereal things that straddle the line between existence and nothingness, but in reality, they're as real as matter itself.
Some physicists have described bosons as weights anchored by mysterious rubber bands to the matter particles that generate them. Using this analogy, we can think of the particles constantly snapping back out of existence in an instant and yet equally capable of getting entangled with other rubber bands attached to other bosons (and imparting force in the process).
Scientists think each of the four fundamental ones has its own specific bosons. Electromagnetic fields, for instance, depend on the photon to transit electromagnetic force to matter. Physicists think the Higgs boson might have a similar function -- but transferring mass itself.
Can't matter just inherently have mass without the Higgs boson confusing things? Not according to the standard model. But physicists have found a solution. What if all particles have no inherent mass, but instead gain mass by passing through a field? This field, known as a Higgs field, could affect different particles in different ways. Photons could slide through unaffected, while W and Z bosons would get bogged down with mass. In fact, assuming the Higgs boson exists, everything that has mass gets it by interacting with the all-powerful Higgs field, which occupies the entire universe. Like the other fields covered by the standard model, the Higgs one would need a carrier particle to affect other particles, and that particle is known as the Higgs boson.
On July 4, 2012, scientists working with the Large Hadron Collider (LHC) announced their discovery of a particle that behaves the way the Higgs boson should behave. The results, while published with a high degree of certainty, are still somewhat preliminary. Some researchers are calling the particle "Higgslike" until the findings -- and the data -- stand up to more scrutiny. Regardless, this finding could usher in a period of rapid discovery about our universe.

In July 2012, the whole world came face to face with the Higgs boson: a sparkly, little light that danced across our screens like Tinker Bell. Wait, that's not right.
While physicists jumped for joy to "see" the Higgs boson -- that elusive particle that composes the Higgs field, which allows particles to gain mass -- the truth is that they actually saw a whole bunch of numbers, graphs and general data that told them that the Higgs boson was detected. And even saying that it was "detected" deserves some explanation.
As reported, the data collected was at 5-sigma levels of certainty. You might've heard that "5-sigma" indicated there was a one in 3.5 million chance the famed boson didn't exist. But not so fast. As with a lot of physics news, it's more complicated than that. The five-sigma confidence level actually meant that there was a one in 3.5 million chance that even if no Higgs particle existed, CERN staff would have seen the same results. In other words, there is a one in 3.5 million chance that an experiment to find the Higgs would come up with results that seemed to confirm it, even if no such particle existed.
So if scientists at CERN (the European Organization for Nuclear Research) weren't expecting to see something that resembled a prop in a stage production of "Peter Pan," what were they looking for? For a long time, physicists were puzzled by the fact that particles like electrons and quarks had mass. They weren't body-shaming the little guys that make up atoms and molecules; it was just that their mathematical representations of a symmetrical universe didn't really work unless the particles were massless [source: Greene].
Peter Higgs and some of his fellow physicists had an idea. Instead of trying to figure out how all these equations could be modified and designed to work with mass-laden particles, why not keep the math and add the assumption that the particles are operating in a field that exerts a drag on them? If that was the case, we might find a substance in this "field" that adds mass to a particle by creating resistance. Imagine a fly buzzing through the air; it's zipping along just fine until it encounters a strong headwind. Suddenly, our speedy, little fly feels quite heavy. So it would be with our particles when they slogged through the Higgs field.
Of course, physicists weren't exactly looking for some sort of universal maple syrup that we'd all been swimming in without noticing. Rather they were searching for particles that might make up a Higgs field, and they thought their search might be successful if they could just recreate the conditions right after the Big Bang. In those conditions, we can see how things like quarks and leptons flew about and if something like the Higgs boson also was created to provide the mass that allows them to clump into composite particles like protons [source: STFC].
The Large Hadron Collider is like a NASCAR track for swarms of racing protons (and some heavy ions, too). Those protons zip in opposite directions around the nearly 17-mile (27 kilometer) circle and run into each other millions of times a second [source: Greene]. When they do collide, the composite particles spray out into their smaller parts -- quarks and leptons. The energy that's created can allow us to see really, really heavy particles created in the collision.
Here's where we start to "see" things like the Higgs boson. The detectors in the LHC measure the energy and charge of the particles that firework out from the proton collisions. The detectors are no shrinking violets -- the biggest one at the LHC is 82 feet (25 meters) tall and equally wide. They need to be that big because gigantic magnets are used to curve the path of particles
If we curve the path of the particles within a magnetic field, we can see how they react differently -- some with really high momentum will still go in a straight line, those with lower momentum will spiral tightly [source: CERN]. So momentum is one helpful piece of information that researchers and physicists can study when puzzling over the identity of a particular particle.
Tracking devices in detectors are handy, too. A tracking device records electronic signals that particles leave behind as they whiz through the detector, which in turn allows a computer to make a graphical representation of the particle's path.
Calorimeters within the detectors also help with identification. A calorimeter measures the energy the particle loses after the collision, and it absorbs the particles within the detector. Physicists can then study the radiation emitted from the particles, which helps them to determine some more unique identifiers for specific particles .
So what does the Higgs boson look like? Well, hate to disappoint, but the whole point is that we can't see it. It's a little particle, man. Don't be crazy. What we see instead is, well, graphs. And data. All that noisy data detailing particle path, energy, decay products and more were swept up in the detectors and synthesized into cold, hard numbers. Those numbers indicated that an "excess of events" took place that indicated the Higgs existence .
Now don't be too disappointed. The nice folks at CERN know what we want: pretty pictures that show a representation of the Higgs boson. If you do want to see a graphical simulation of the collisions, check out the CERN website for some (very satisfying) representations of what Higgs "looks" like in action .

Copyright © 2011 - All Rights Reserved - Softron.in
Template by Softron Technology